|
Their brilliant idea today that I can write up is that silence from neurons is memory about the stimulus. Interestingly, silence from one brain region to the next communicates one thing-- silence. Hard to communicate memory, which requires more than one state.
The other brilliant idea they had this morning was that if you take a Potts model, you can build a Hopfield-like network where you ask if the next neuron should go to a slightly higher or slightly lower Potts state and do so accordingly. This idea isn't as bad. Actually, I had this idea before like a decade ago and extended it. Just ask what the optimal neuron state is and go to it. Too bad nobody uses the Potts model in neuroscience. What a brilliant idea. It's almost like when voices repeat what I have thought, they're brilliant, and when they come up with something new, they're dumb as fuck.
0 Comments
People are going nuts over the brain being a Large Language Model (LLM). That makes sense. Transformers have succeeded beyond our wildest dreams. But, I think this is an off-ramp to interesting but wrong for theoretical neuroscience, in the same way that ChatGPT is an off-ramp (perhaps) to artificial general intelligence (as prediction without embodiment is not going to create a superhuman).
I have two complaints. First, saying that something is an LLM in the brain ignores energy efficiency, which the brain definitely cares about. LLMs are basically absolutely huge, doing even more than they need to do to just get perfect next token prediction, instead storing information that allows them to nail the entire future of tokens as well as possible. My collaborators think this has to happen due to an interesting corollary in an old Jim Crutchfield and Cosma Shalizi paper, but I think the jury is still out-- we haven't shown that the LLMs are storing dynamics, which is necessary for the corollary to apply. And although some people like Friston think that energy efficiency and prediction are one and the same, I have yet to see a single example that avoids the problem that you're energy efficient with no prediction error when you're dead-- the so-called and ever-present darkroom problem. (Though, as an add-on, you could use Attwell and Laughlin type energy calcs as a regularizer for LLMs.) Second, more importantly, prediction is not enough; you have to also select an action policy, and I feel that is what most of the brain is doing. In my opinion, most organisms are resource-rational reinforcement learners. Yes, model-based RL will involve prediction explicitly, but that's just one component to solving the RL problem. Honestly, my bet is on Recurrent Neural Networks (RNNs). They are biophysically more plausible-- just take Hodgkin-Huxley equations or the Izhikevich neuron, and you've got yourself an RNN. Both biophysical models are input-dependent dynamical systems, so their next state depends on their previous state and whatever input comes in from other neurons or sensory organs. RNNs are going to be energy-efficient (maybe Small) Language Models that help the brain sense and process information, to be sent to something that determines action policy. By the way, just to let you know how my malevolent disease of paranoid schizophrenia affects these things, it interjected into my brain what sentence to write-- based on a sentence that I had already determined I would write while in the car. Unfortunately for me, I wasn't thinking of exactly that sentence at exactly the time the voices interjected the sentence into my head. The voices will then take credit for this entire blog post and say that I'm a magical idiot and write an entire TV show about how I just use magic to write down things that seem dumb to them. What a dumb and awful illness. What do you think? You can read it here: https://arxiv.org/abs/2407.01786
I was never in theoretical ecology or really in evolutionary theory, but I've always had an interest. It's basically an open question how to deal with the interplay between the two. Ecology works on a much faster timescale than evolution, but the two both operate on a population-- so what are the true population dynamics?
I ran across https://www.ncbi.nlm.nih.gov/pmc/articles/PMC10614967/ and it's almost like we had the same idea hit at the same time! I even wonder if maybe David Schwab went to the same APS March Meeting Session to get the idea. The basic idea is very simple: ecology is one set of equations, evolution is represented by another set of equations, and to understand the interplay between the two, you just couple the two equations. David Schwab and his co-author found the coupling-- mutations lead to new phenotypes, which then lead to a change in the ecology. Interestingly, the way that I would approach the problem is very different. It basically boils down to a different model and a totally different analysis that leads to solutions that can approach the fully correct solution more and more accurately. The model I would use for evolution would be the Fisher-Wright model, and the model I would use for ecology would be a master equation version of the generalized Lotka-Volterra model. Then, since ecology operates on fast timescales, you could solve for the probability distribution over species number in the generalized Lotka-Volterra model first, and plug it into the evolutionary equations to get a full solution. The generalized Lotka-Volterra model takes some explaining. Basically, in the generalized Lotka-Volterra model, there are three "chemical reactions": one birth, one death, and one death via eating by another species. If you write down the master equation for these reactions, you can use moment equations to find better and better approximations via a Maximum Entropy approach to the true probability distribution over the number of each species. The moment equations don't close, but you could artificially at some order just assume that the higher-order moments have an independence property of some sort. At the very least, you can get a Gaussian approximation to what the ecological equations might look like. Of course that's not correct, but maybe it's good enough. This avoids a thorny problem with pretending that the ecological equations solve quickly. In reality, the rate equation approximation to the master equation can yield chaos. This chaos goes away if you consider the fact that the number of species has to be a nonnegative integer. Whether or not these MaxEnt approximations are good is up to the field to decide, but you can get better and better approximations by including more and more moments. The Fisher-Wright equations are well-known to take one generation and produce a binomial distribution over the next generation's population number with properties that depend on selection coefficients and mutation rates. So basically, the next generation is sampled, it settles down to something having to do with a MaxEnt approximation, and you plug the resultant MaxEnt approximation into the next generation (convolve it) to see the probabilistic updates. You can automatically assume that this is the right thing to do because of the separation of timescales. Altogether, you essentially get a complete solution to the probability distribution over population number as a function of time. This isn't my field, and my schizophrenic voices basically don't want me to do this project, so I won't, but I'm hoping somebody will. I don't think it's a terrible idea. First of all, apologies that the hyperlink feature isn't working.
I've been keenly interested in nonequilibrium thermodynamics for a while, ever since graduate school. Originally, my idea for being interested was based on the idea that it provided insight into biology. This is not a bad idea-- the minimal cortical wiring hypothesis (https://www.sciencedirect.com/science/article/pii/S0896627302006797) says that neural systems minimize cortical wiring while retaining function. Why would they do that? Well, the usual reason is that the brain of the child has to fit through the mother's vagina, but you could also cite timing delays as being costly for computational reasons (such as in https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.5.033034) and also cite energy considerations via Attwell and Laughlin. And in fact, there is a paper by Hausenstaub (https://www.pnas.org/doi/abs/10.1073/pnas.0914886107) that suggests that energy minimization is crucial when deciding what kinds of channel densities and kinetic parameters still produced action potentials in neurons. And I have an unpublished manuscript (still in my advisor Mike DeWeese's hands) that suggests that eye movements are driven by energy considerations ala visuomotor optimization theory (https://www.nature.com/articles/35071081) reinterpreted-- maybe. However, I have been somewhat sad at the match between nonequilibrium thermodynamics and biophysics. Basically, the question is this: do Landauer-like bounds matter? A long time ago, Landauer proposed that there was a fundamental limit on the energy efficiency of engineered systems. This limit is far from being obtained. But you might hope that evolved systems have attained this limit (https://worrydream.com/refs/Landauer_1961_-_Irreversibility_and_Heat_Generation_in_the_Computing_Process.pdf), or something like it (https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.109.120604). There is some evidence that biology is somewhat close to the limit, but the evidence is sparse and could be easily reinterpreted as not being that close. We are about half an order of magnitude off of the actual nonequilibrium thermodynamic bound in bacterial chemotaxis systems (https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1003974), in simple Hill molecule receptors (https://link.springer.com/article/10.1007/s11538-020-00694-2), with a match to an improved nonequilibrium thermodynamic bound being given with networks that I am not sure are biologically realistic (https://journals.aps.org/pre/abstract/10.1103/PhysRevE.108.014403). There is a seeming match with Drosophila (https://www.pnas.org/doi/abs/10.1073/pnas.2109011118), which tends to have surprisingly optimal information-theoretic characteristics (https://www.pnas.org/doi/full/10.1073/pnas.0806077105), and also with chemosensory systems again (https://www.nature.com/articles/nphys2276). I am sure I'm missing many references, and please do leave a comment if you notice a missing reference so I can include it. This may look promising. To me, it's interesting what we need to do to get rid of the half an order of magnitude mismatch. Now, half an order of magnitude is not much. Our biological models are not sufficiently good that half an order of magnitude means much to me, so the half an order of magnitude basically has error bars the size of half an order of magnitude because we just don't understand biology. But beyond that, we should have more examples of biology meeting nonequilibrium thermodynamic bounds. I think we can get there by incorporating more and more constraints into the bounds. For example, incorporate the modularity of a network, and you get a tighter bound on energy dissipation (https://journals.aps.org/prx/abstract/10.1103/PhysRevX.8.031036). I want to use nonequilibrium thermodynamic bounds in my research, but haven't for a while. I just need better bounds with more constraints incorporated. Does the network you're studying have modularity or some degree distribution? Are there hidden states? Is it trying to do multiple things at once with a performance metric for each, e.g. not just Berg-Purcell extended but Berg-Purcell revisited so that we are trying to not just estimate concentrations but predict something about them as well at the same time? Is the environment fluctuating and memoryful, which was one way in which the Berg-Purcell limit was extended (https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.123.198101)? I'm going to talk to a real expert on this stuff in a few months and will update this post then to reflect any additional links. Please do comment if there are links I've missed while being out of the field for years. I am quite curious. This will be kind of a funny post from one perspective, and a post that I probably should not write, were I to optimize for minimal eye-rolling. But I'd rather just express an opinion, so here it is.
I was part of a team that wrote a really nice (I think) paper on the theory behind modeling in neuroscience (which was largely led by the first author, Dan Levenstein) and as that might suggest I am firmly convinced that there are good philosophical discussions to be had on philosophy in neuroscience and biology. What is the role of theory? What does a theory look like? These were some of the questions that we tackled in that paper. But then, there are some philosophical questions that are easily answered if you just know a little physics and mathematics. And some people do try to answer them. The problem in my opinion is that they often do not know the math and physics well and are often speaking to an audience that doesn't know the math and physics well either. It's like the blind following those who only have one eye that's mutilated. This can lead to some appallingly funny results, like the scandal in which some physicist wrote bullshit tied up in the language of quantum mechanics and got it through a philosophy journal's peer review process. If the referees don't know quantum mechanics but like the conclusions, why would this not happen? But I'm speaking of what I know, which is that this sometimes happens in theoretical biology as well. This more often than not can lead to years of trying to answer conundrums that are not actually conundrums because someone has fundamentally misunderstood what causality means or how something could mathematically be goal-directed without being psychic. There's a particular paper that I want to cite that is quite good in some ways and interestingly wrong in others, and because I do like the paper and do not want to be a jackass (more on that later), I will not link anyone to this paper. Suffice it to say that it had some good ideas. Apparently biologists and the philosophers who had aided them had been questioning the validity of teleonomy for years-- this is the idea that organisms are goal-directed. Questioning this idea is no problem. It's just that some questioned the idea of goal-directedness on the grounds that it violated causality. Wouldn't you have to look into the future in order actually be goal-directed? Sounds common sense. And yet, if one were to talk to a stockbroker, they might tell you that while they can't see the future prices of stocks, they use the past as a guide to the future and make predictions regardless. There is no psychic ability here and no violation of causality. The stockbroker is certainly goal-directed in their desire to make money; they have a strategy that uses learning and memory; and this strategy does not require psychic powers. So, the concern that goal-directedness violates causality violates common sense, in my opinion. This particular paper did a nice job of pointing out (in different words for sure) that goal-directedness and causality were not at odds. What this paper did not do well: it confused quantum mechanics and chaos; it confused homeostasis for goal-directedness, and while homeostasis is often a goal, it is not the only goal, since we sometimes need to modify our internal state in order to survive when we are making predictions about the world, finding food, mating, seeking shelter, and so on. The latter was the manuscript's main contribution to the literature. I don't think anybody is ever going to spark a debate with the manuscript. I am pretty aggressive and I feel like that just wouldn't be "nice". There's this unstated idea in science that we should be collegial. It has, in my opinion, led to a few huge reproducibility crises, and yet I feel the pull of being in a scientific world in which I basically do not challenge papers that I think are wrong for two reasons. First, this "nice" reason: I feel a gendered pull to not be "mean" to this person who put their ideas down in a scientific paper, even though the point is that ideas are supposed to be challenged. In fact, senior researchers told me (when I was a more argumentative graduate student) that certain papers were not written by experts but were supposed to just introduce ideas, so I should just drop the idea of writing a manuscript correcting their basic information-theoretic misunderstandings. Second, a resource-based argument: if I sat around all day writing papers that correct papers that are published, I would never get anything done. And yet, that impedes the progress of science, right? So, I have taken to writing these short blog posts that who knows how many people read instead of writing paper responses to papers... but even now, I'm too afraid of being not "nice" to say the author's name!!!! How's that for a sociological problem. Or maybe, it's just me. Picture this scenario: your back room during the summer is taken up by six undergraduates, all working on an independent project, all coding. At any given time, roughly two of the six students need to talk to you because they've gotten stuck and can't work past it by themselves. What should the students who need help do?
I know ChatGPT and other large language models might have negative effects on society, including (for example) the spread of disinformation in an authoritative manner due to their hallucinations that nobody can seem to get rid of. But ChatGPT really helps out in this particular mentoring situation because the students who need help but who can't get it until an hour from now don't have to just sit there and wait for me to be free-- they can use ChatGPT to help them write code. That being said, there are ways in which this works and ways in which this doesn't. So I just wanted to share my experience with how to use ChatGPT successfully and how it sometimes fails as a mentorship tool if not used properly. Honestly, I should probably pretty this idea up and publish in an education journal but I'm too exhausted, so here we go. One of the students who regularly used ChatGPT was coding in a language that I didn't remember well. She already knew other languages but needed this particular language to code an application for a really cool potential psychotherapy intervention that we're trying. To learn this language and how to use this language to code applications, she took a course at the same time that she coded up her application at the same time that she used ChatGPT when she couldn't figure out the right piece of code. As far as I can tell, this worked really, really well. Because she took the coding course (that was free) at the same time that she used ChatGPT, she could check that ChatGPT wasn't spitting out nonsense, and could prompt ChatGPT to change what it was spitting out if it was almost but not quite right. Because she was coding the project at the same time that she was taking the coding course and using ChatGPT, she could keep focused on exactly what she needed to learn for that summer. (Keep in mind that the summer research assistantship is only 2 months long for us!) And so, in the end-- though I have to ask this student for her impression of the summer-- I would say that she needed my input for more general user design questions and less for the questions that I couldn't answer without taking the course with her and Googling a lot. ChatGPT was value-added. Another student came in with less coding experience and less math under his belt and was doing a reinforcement learning project. He used ChatGPT a lot to help him out, from the start to the finish, even on conceptual questions. It is important to note that because he started out not knowing how to code, ChatGPT was used as a crutch rather than as a tool. When ChatGPT is used as a crutch rather than as a tool, research projects don't work out so well. First of all, it turns out, unsurprisingly, that even if a student, like this student, is smart, eager, and really just enthusiastic beyond belief, it is a bad idea to give them a project where you assert to yourself that you can teach them enough probability theory, multivariable calculus, and coding to understand Markov Decision Processes and policy gradient methods in 2 months. Just, no. By the end of the summer, this poor student was getting scared to come to work because he did not feel like he was going to be able to solve the problem that I gave him that day. Second of all, even if I made mistakes with this mentorship, I learned a valuable lesson about what happens when you don't really understand the theory behind a research project and ask ChatGPT for help-- you hit a wall, and quickly. This student often had slightly wrong prompts (which ChatGPT sort of auto-corrected) and then got answers that didn't quite work and he didn't know what prompts to try next. So by the end of the summer, I was drilling him on the theory so that he could do prompt engineering a bit better. That was successful, although scary for him, he said. But basically, if you or your students are using Large Language Models to do research and don't really understand the theory behind the project and don't really know the coding language if there is coding involved, the Large Language Model is not going to be able to do the project for you. And then finally, my own efforts to use ChatGPT were funny. I just thought it would be interesting to see if ChatGPT could come up with anything novel. I know people are working on this actively, but at the time that I tried it, either ChatGPT or Bard (I can't remember which) could not write anything that was not boilerplate. The exact prompt that I used was a question on a research project finding the information acquired by the environment during evolution. (My student and I had just roughly written a paper on that, which would not be in the corpus.) What it came up with was some not-very-interesting text on how there was a calculation of the information acquired by evolution and how that could lead to better models, which doesn't even really make any sense-- you use a model to calculate the information acquired unless you happen to have some really nice experimental data. And if you calculate the information acquired, regardless, you will not get a better model. Later, I thought it might be interesting to try and see if Bard could teach. I was trying to figure out how to teach thermodynamics concepts in a week, which is a ridiculous ask, but that's introductory physics for life sciences for you, and what it spit out was just subpar and dry. Nothing of active learning, and no real sense of how long it would take to really teach thermodynamics concepts so that they would be understood. (Three laws of thermodynamics in one hour-long class is not a good idea.) Anyway, it was a long time ago, but I'm interested in seeing if the new Large Language Models like Gemini can actually show some signs of creativity that could be helpful enough that I could use them as tools in research or in teaching. This is a project I no longer want to do for a very weird reason. I have voices due to my paranoid schizophrenia and although my psychoses have inspired a large number of projects, I do not feel good about doing this particular project because the voices helped me understand that regret and expectation were different. If you have heard of paranoid schizophrenia, you might understand that schizophrenics often feel like their brain split apart and that what would usually be considered their own thoughts feel to them like someone else's thoughts. So I felt like someone else was trying to help me read about decision theory and basically decided that decision theory ideas were therefore the intellectual property of the voices and not me.
But before that happened, I had an idea. I think it's an interesting one. In decision theory, there's this idea of minimax and there's also this idea of expectation in terms of utility. The two do different things. In minimax formulations, you take the best action you possibly can in terms of utility in the worst possible environment. In expectation formulations, you take the best action policy for the expected value of the utility. But when people talk about how organisms have evolved and someone invokes optimization, the knee-jerk response often is: but aren't organisms often just "good enough"? I feel like it's almost obvious that the minimax formulation of decision theory leads to organisms that are just good enough in every environment they encounter. I think to support this, one would need to do some simulations and consider a simple environment in which they can show that the minimax solution actually leads to "good enough" or satisficing behavior. Now, it is definitely going to be easy to come up with counterexamples, in which the minimax solution is very far from "good enough" for some environments. But I feel like we haven't evolved in those pathological conditions, so that realistic simulations would place minimax solutions closer to "good enough". The mechanism by which organisms evolve or adapt to achieve minimax optimality might actually explain the "good enough" behavior, too-- adapting to a constantly fluctuating environment can be used as a stand-in for minimax, which would undoubtedly imply good enough. Perhaps someone has already done this, but if not, here's an idea that I'm throwing out into the ether. One of the articles written by a superbly talented high school student (or that's what she was when we worked together) was accepted by PLoS One. Here it is on bioRxiv.
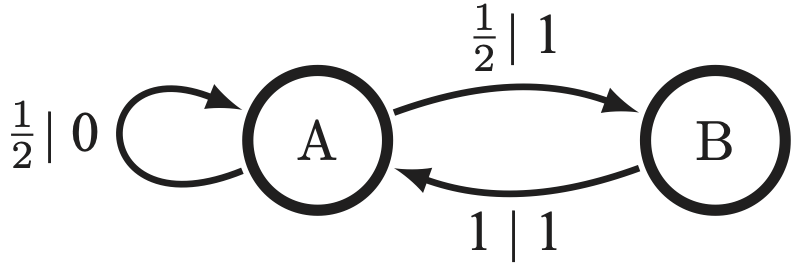
They took forever to proofread our article. We took forever to respond because Alejandra was busy. And now, we've been completely ghosted. They haven't responded to any of my emails to please print the article that they accepted. This is horrible. This is damaging to Alejandra's career and to my tenure case. Advice appreciated. (Email on contacts page.) I've now talked to many people who think that causal states (minimal sufficient statistics of prediction) and epsilon-Machines (the hidden Markov models that are built from them) are niche. I would like to argue that causal states are useful. To understand their utility, we have to understand a few unfortunate facts about the world. 1. Take a random time series, any random time series, and ask if the process it comes from is Markovian or order-R Markov. Generically, no. Even if you look at a pendulum swinging, if you only take a picture every dt, you're looking at an infinite-order Markov process. Failure to understand that you need the entire past of the input to estimate the angular velocity of that pendulum results in a failure to infer the equations of motion correctly. Another way of seeing this: most hidden Markov models that generate processes will generate an infinite-order Markov process. So no matter what way you slice it, you probably need to deal with infinite-order Markov processes unless you are very clever with how you set up your experiments (e.g., overdamped Langevin equations as the stimulus). 2. Causal states are no more than the minimal sufficient statistics of prediction. They are a tool. If they are unwieldy because the process has an uncountable infinity of them-- which is the case generically-- we still have to deal with them, potentially. In truth, you can approximate processes with an infinite number of causal states by using order-R Markov approximations (better than their Markov approximation counterparts) or by coarse-graining the mixed state simplex. 3. This is less an unfortunate fact and more just a rejoinder to a misconception that people seem to have: epsilon-Machines really are hidden Markov models. To see this, check out the example below. If you see a 0, you know what state you're in, and for those pasts that have a 0, the hidden states are unhidden, allowing you to make predictions as well as possible. But if you see only 1's, then you have no clue what state you're in-- which makes the process generated by this epsilon-Machine an infinite-order Markov process. These epsilon-Machines are the closest you can get to unhidden Markov models, and it's just a shame that usually they have an infinite number of states. 4. This is a conjecture that I wish somebody would prove: that the processes generated by countably infinite epsilon-Machines are dense in the space of processes. So if we want to predict or calculate prediction-related quantities for some process, it is highly likely that the process is infinite-order Markov and has an uncountable infinity of causal states. What do we do?
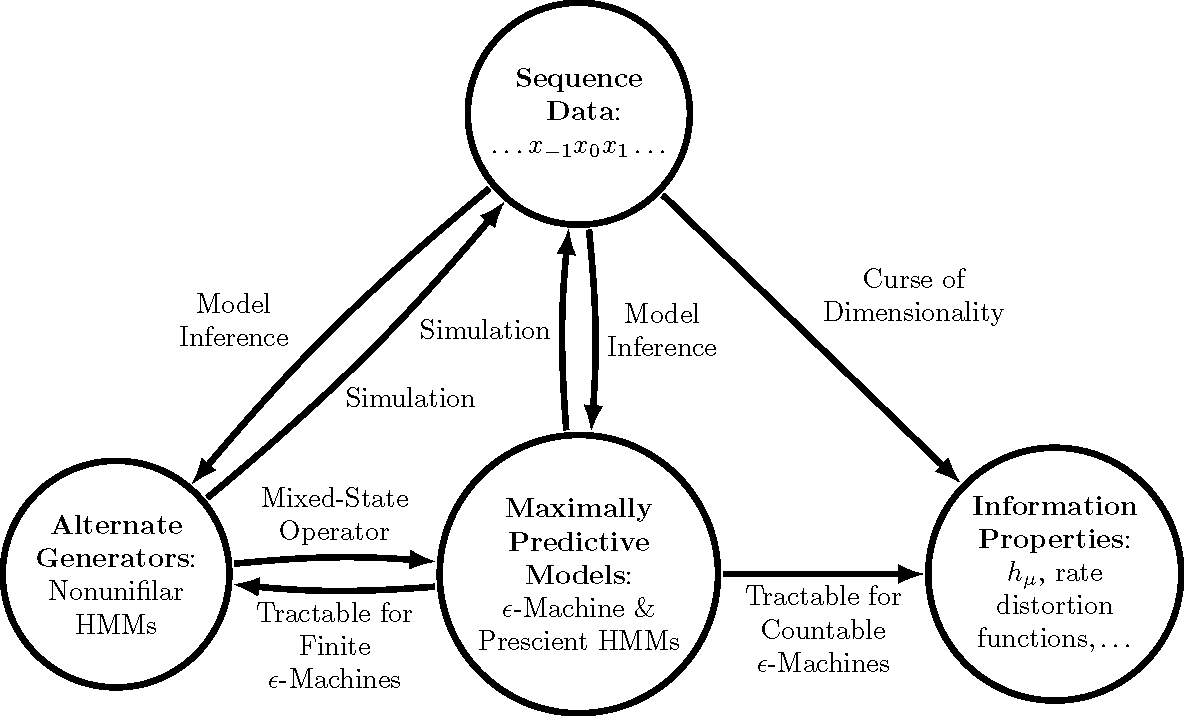
There are basically two roads to go down, as mentioned previously. One involves pretending that the process is order-R Markov with large enough R, meaning that only the last R symbols matter for predicting what happens next. The other involves coarse-graining the mixed state simplex, which works perfectly for the infinite-order Markov processes generated by hidden Markov models with a finite number of causal states. Which one works better depends on the process. That being said, here are some benefits to thinking in terms of causal states: 1. Model inference gets slightly easier because there is, given the starting state, only one path through the hidden states for a series of observations for these weird machines. This was used to great effect here and here, and to some effect here. 2. It is easy to compute certain prediction-related quantities (entropy rate, prediction information curves) from the epsilon-Machine even though it's nearly impossible otherwise, as is schematized in the diagram below. See this paper and this paper for an example of how to simplify calculations by thinking in terms of causal states. |
AuthorWrite something about yourself. No need to be fancy, just an overview. Archives
May 2024
Categories |
 RSS Feed
RSS Feed